بروزرسانی: 26-2-1397
کنترل آشوب
|
معرفی به دلیل دینامیک پیچیده و ناپایداری ذاتی سیستم آشوبی، ایده ی کنترل آن به طوری که رفتار مورد نظر را از خود نشان دهد، غیر ممکن به نظر می رسد. با این حال در مراجع مختلف نشان داده شده است که سیستم های آشوبی قابلیت کنترل شوندگی دارند و اهداف کنترلی متفاوتی برای این سیستم ها قابل تصور است که می توان به موارد زیر اشاره کرد:
یکی از روش های مهم و پرکاربرد در حذف رفتارهای نا به هنجار سیستم آشوبناک، پایدارسازی آن است. پایدارسازی به دو دسته تنظیم و تعقیب تقسیم می شود. در مسئله ی تنظیم، سیستم را با اعمال قانون کنترل مناسب به یکی از نقاط تعادل و یا به یکی از مسیرهای متناوب ناپایدار موجود در جاذب عجیب (ایجاد چرخه ی حدی پایدار) سیستم آشوبناک پایدار می کنند. این نوع پایدارسازی در کنترل راکتورهای شیمیایی ، نوسان سازها و مدارات الکتریکی ، لیزرها، مخابرات راه دور، حذف نویز و ... کاربرد دارد. دسته ی دیگری از مسائل پایدارسازی سیستم های آشوبناک، مسئله ی تعقیب می باشد. در این نوع پایدارسازی ، یک سیگنال مرجع متغیر با زمان در نظر گرفته می شود و قانون کنترل طوری طراحی می شود که پاسخ های سیستم ، سیگنال مرجع را دنبال کنند. موارد اول و دوم واضح اند، سیستم دارای رفتار آشوبی است و این رفتار برای ما مطلوب نیست. به عنوان مثال، اگر نوسان آشوبی غیر قابل قبولی در روتور یک موتور باشد، حذف آن ضروری است. همزمان سازی دو سیستم آشوبی به این معناست که بخواهیم حالت دو سیستم آشوبی دقیقا مشابه هم شوند. از طرفي در سال هاي اخير كاربردهاي فراواني بوجود آمده اند كه در آن ها حالت مطلوب سيستم به شكل يك رفتار آشوبناك توصيف مي شود. مسئله كنترل در مورد اين سيستم ها به صورت تبديل يك رفتار آشوبناك ناخواسته به شكل يك رفتار آشفته با خصوصيات تعريف شده ومطلوب بيان مي گردد.
مدل دینامیکی سیستم آشوب نمونه به صورت زیر است:
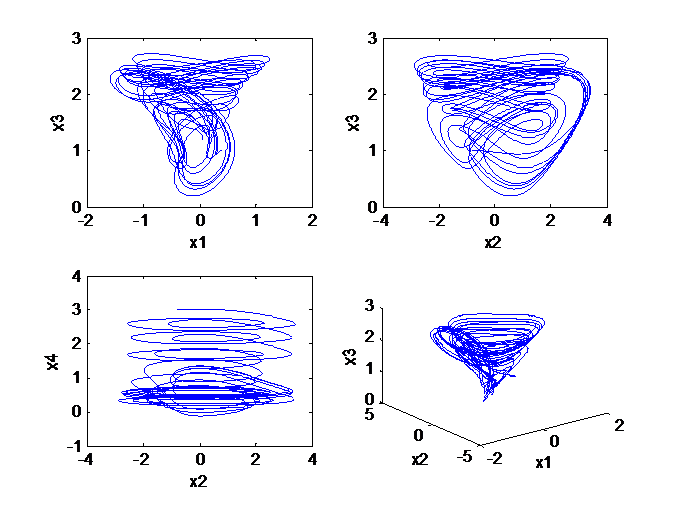 |
|
|
بازدید امروز: 4